Have you ever played a chance game? Lottery, pick-a-card, and spin the wheel are all examples of games based on chances and what many call the “game of luck”; however, many may not know how simple games of chance could create discord among science, the same way it does to arcade ‘luck’.
Predictions happen because every event is ordered or ‘predestined’. When you drop a ball, the ball falls because of gravity. When you ring a bell, the bell creates a sound that will jingle and bounce to different areas of the room to hear. Because everything is ordered, there are predictions, and because there are predictions, there exist the ‘fight of fate’ as fiction writers love to call; however, if humans would create enemies with other humans as a matter of fighting for the right prediction the same way many mathematicians and scientist have done, then even the concept of prediction has its own foe: chaos.
In this article, we’ll take a quick look at a developing theory known as “chaos theory,” which demonstrates how even predictable events may prove unpredictable. Consider a specific circumstance represented by a ball. If one has knowledge of the ball’s origin (before its descent) and its release time, they can make an accurate prediction. There’s an increased likelihood that the precise position is near the actual position if both of the above are known.

Now see the ball as a component of a scatter ball game. The ball may fall on either side of the board at any level, and any minor variation in the ball’s experience will result in a different conclusion. Its path and final resting spot are now contingent upon the initial conditions being extremely within. Similar to this, chaos theory is a significantly limitless board.
If there is uncertainty of the ball’s initial position, then its ultimate route is unknowable.
Despite what was previously said, chaos doesn’t always have to be as perplexing as it sounds. Mathematically, it may be understood quite easily using a system known as a logistic map. Using a logistic map only requires multiplying three integers together. The input, which we refer to as x, will range from 0 to 1. This is comparable to the initial location of the ball. We could begin with an input of 0.25, for instance. The second figure is 1 – x, or 0.75 in this particular case. The parameter, which is represented by r, is the third integer and is necessary to finish the system. Throughout the operation, this value remains constant and describes the layer of the peg-board.
We will start by considering the system has r = 2.
Then the input is χ, and the output r * χ * 1 (1 – χ) or can also be written as:
χ→ r * χ* (1- χ)
As x approaches the parameter multiplied by the first and second data.
We refeed the output as an input to carry on the operation. This entails mixing the three elements once more: 1 – 0.375 =0.625; r, or 2 ; and the new input, 0.375. The next output is 2 * 0.375 * 0.625 = 0.469 (to three decimal places) as a result.
Now, if we re-input this, we will receive an output of 0.498, which is followed by a value that is extremely near to 0.5. The result of performing this procedure is a sequence that looks like this: 0.25, 0.375, 0.498, 0.500,… As the process continues, the sequence approaches the number 0.5, which is known as the system’s attraction point. The sequence will always zero in on its attractive point, which is 0.5, regardless of where we start the system (as long as the parameter is between 0 and 1). This is comparable in mathematics to letting a ball fall flat on the ground.
The interesting part here is when we alter r and input a number greater than 0 and 1, such as 3.3 and subject it to the same process. With the initial value of 0.25, we get a new sequence:
0.25, 0.62, 0.78, 0.57, 0.81, 0.51, 0.82, 0.48, 0.82, 0.48, 0.82, 0.48, 0.82…
As the process runs, this time it does not settle with one attracting point but two of them which are 0.48 and 0.82. This is called an attracting 2-cycle system. Moreover, if we increase the value of r as 3.5, and restart the process again: there will be an attracting 4-cycle system in the numbers 0.50,0.87,0.38,0.83. We can see that as r increases, the attracting cycle system doubles. Systems exist with attracting 8-cycles, 12-cycles, 64-cycles, and so on.
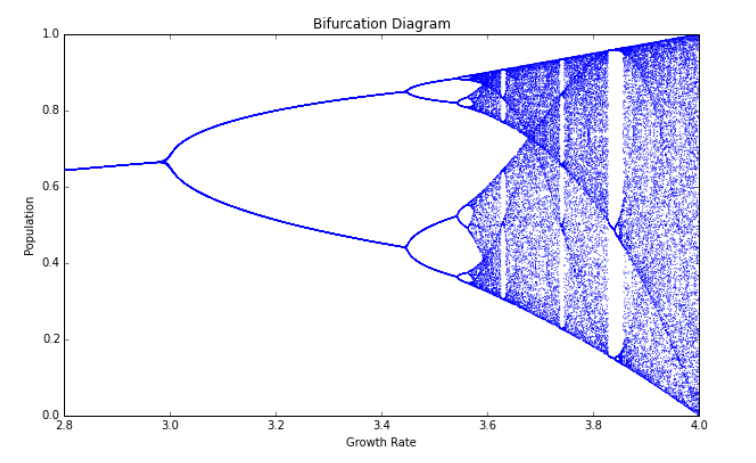
Still, this stops as well. When r exceeds 3.57, we have a completely different phenomenon. Suppose we take r = 3.7 and restart the process we get:
0.25, 0.69, 0.79, 0.62, 0.87, 0.42, 0.90, 0.33, 0.82, 0.55, 0.92…
If you feel that even if you let this sequence run forever, in some areas, there will be a pattern; that’s not the case. In actuality, this sequence is chaotic because, even if it continues indefinitely, it will never settle into a particular pattern. Furthermore, the new sequence will ultimately appear completely different from the original, much like the butterfly effect, if we alter the input even slightly.
In summary, if there are predictions because of a constant and recurring pattern, then there is also chaos which has no definite pattern at all. Just like in mathematics, chaos revolves around infinity and randomness with a slight change creating something hugely unsystematic. Still, even if this side of mathematics continues to spread its ambiguity and disorder, it doesn’t mean it cannot be understood.
Works Cited
Boeing, G. (2015, March 26). Chaos Theory and the Logistic Map. Geoff Boeing. https://geoffboeing.com/2015/03/chaos-theory-logistic-map/
Oestreicher, C. (2007). A history of chaos theory. Dialogues in Clinical Neuroscience, 9(3), 279–289. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3202497/The Editors of Encyclopedia Britannica. (2019). chaos theory | Definition & Facts | Britannica. In Encyclopædia Britannica. https://www.britannica.com/science/chaos-theory
About the Author
My name is Xiu Ann, I’m a senior STEM student from the Philippines currently studying pathology. I have published a research about geodetic engineering science, and a few research syntheses from our school. I hope this article has spread knowledge, and helps in creating a cause of movement for the people searching for a truth.

Leave a comment